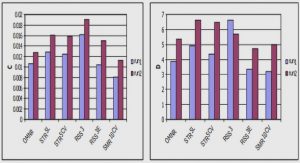
- Wednesday
- April 30th, 2025
- Share Files

Get Complete Project Material File(s) Now! » Diagrammatical description of Br,s p q Aside from the definition of Br,s p q as a factor-algebra of Br,s, there is also a convenient graphical presentation for a basis of Br,s p q...

Get Complete Project Material File(s) Now! » Displacement fields As usual, by rigid motion we mean the space R(Q) := r ∈ H1(Q;R3) : e(r) = 0 namely vector fields of the form r(x) = a + b ∧ x,...

Get Complete Project Material File(s) Now! » Previous Works This chapter somehow creates a new problem instead of solving an existing one. This justifies the shortness of this section. Discrete Morse theory was introduced in [49, 50]. It was then...

Get Complete Project Material File(s) Now! » The optimal transport problem and Wasserstein spaces The optimal mass transfer problem was first introduced in 1781 by Gaspard Monge in his “Mémoire sur la Théorie des Déblais et des Remblais”. The seminal...

Get Complete Project Material File(s) Now! » Physical and geometrical set-up Let us consider an incompressible, homogeneous, and ideal uid, of constant density , in a domain (t). At the time t 2 [0; T), the domain occupied by the...
Get Complete Project Material File(s) Now! » Classification of mathematical programming problems In this section we propose a classification of MP problems. Before doing that, a very important concept must be introduced: convexity. Note that in the rest of this...

Get Complete Project Material File(s) Now! » Computational burden of the Monte-Carlo estimator For the Monte-Carlo estimator, when pf << 1 the coefficient of variation satisfies Making the approximation CV = p 1 pfNf , a condition CV < c...

Get Complete Project Material File(s) Now! » Intractability of unordered regular expres-sions In this section, we study the reasons of the intractability of UREs w.r.t. the following two fundamental decision problems: membership and containment. In Section 1.3.1 we show that...

Get Complete Project Material File(s) Now! » Bounds from derivation of the Chow form The first application of this technique is to obtain bounds for primitive element representa-tion (see Subsection 2.1.2) using the analogy of the Chow form and the...