Get Complete Project Material File(s) Now! »
Vérification de l’approximation des pores irréguliers par des ellipsoïdes
La meilleure technique pour vérifier mécaniquement l’approximation des pores par des ellipsoïdes est de comparer les tenseurs de contribution des pores (souplesse élastique et résistivité thermique) avec ceux des ellipsoïdes. Il s’agit là du 2ème problème d’Eshelby où une matrice élastique infinie est considérée, contenant une hétérogénéité constituée par un matériau élastique ayant des propriétés différentes, et soumise à une charge uniforme (contrainte ou déformation) aux limites infinies.
On considère deux problèmes : le problème d’élasticité et le problème de conductivité thermique. Les tenseurs de contribution (souplesse pour l’élasticité et résistivité pour la conductivité thermique) des pores irréguliers sont évalués par le biais d’une méthode numérique et deux méthodes analytiques :
• Méthode numérique
Cette méthode est utilisée dans le cas élastique et thermique pour les pores irréguliers comme pour les pores ellipsoïdaux. Elle est basée sur la méthode des éléments finis (FEM) en considérant le problème de l’inhomogénéité de forme irrégulière (ou ellipsoïdale), isolé dans une matrice infinie (Figure 0.8). Les résultats sont obtenus à partir d’une intégrale d’un produit vectoriel sur le volume de l’hétérogénéité comme suit :
Figure 0. 8: Le maillage de la surface et du volume du pore irrégulier et ellipsoïdal dans un cube de référence à l’aide des éléments quadratiques pour les simulations numériques élastiques et thermiques.
Pour le problème élastique, le produit vectoriel correspond au produit du vecteur de déplacement et du vecteur normal. Le vecteur de déplacement est calculé à partir des simulations numériques mécaniques et le vecteur normal est calculé à partir du produit de 2 vecteurs directeurs de la surface du pore :
où et sont des coordonnées curvilignes d’un plan de référence local défini.
Pour le problème de conductivité thermique, le produit vectoriel correspond au produit du vecteur de température et du vecteur normal.
• Méthode analytique basée sur la fonction explicite de l’ellipsoïde
Pour vérifier l’approximation des pores par des ellipsoïdes, on a évalué ensuite les tenseurs de contribution de souplesse et de résistivité thermique pour les ellipsoïdes avec la même procédure numérique d’une part, et en utilisant une solution analytique en calculant le vecteur normal à partir de la fonction implicite de l’ellipsoïde f ( z1 , z2 , z3 ) 0 . Le vecteur normal unitaire à la surface de l’inhomogénéité est alors proportionnel au gradient de la fonction scalaire.
• Méthode analytique basée sur le premier problème d’Eshelby
Une autre solution analytique peut être obtenue pour le cas élastique seulement en considérant le cas d’une inclusion ellipsoïdale intégrée dans une matrice. Par conséquent, la relation entre les tenseurs d’Eshelby et de Hill est donnée par l’équation suivante dans le cadre du premier problème Eshelby:
où ℙ est le tenseur de Hill, est le tenseur d’Eshelby et ℂ est le tenseur de rigidité élastique. L’indice «0» se réfère à la phase matricielle et l’indice «1» se réfère à la partie d’inclusion. Ainsi, l’importance du premier problème Eshelby est due à la détermination du tenseur de contribution de la souplesse en fonction des tenseurs Hill et Eshelby, c’est-à-dire pour l’inclusion ellipsoïdale, la solution des tenseurs de souplesse peut être obtenue analytiquement comme suit :
où N est un tenseur constant de quatrième ordre dépendant de la forme et donné par:
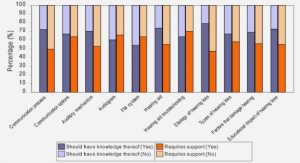
Le tableau 0.1 montre 10 pores sélectionnés dans le VER du calcaire du Lavoux, ainsi que les approximations ellipsoïdales correspondantes avec les valeurs des erreurs relatives entre les différentes valeurs des tenseurs numériques et analytiques obtenus dans les 2 cas élastique et thermique. Le calcul de l’erreur se fait par rapport à la solution analytique d’Eshelby dans le cas élastique et à la solution analytique à partir de la fonction implicite de l’ellipsoïde dans le cas thermique car ces deux solutions ne dépendent pas du maillage du modèle. Les résultats montrent un écart de 5% maximum dans le cas élastique et de 12% dans le cas thermique entre les résultats analytiques et numériques, ce qui rend l’approximation effectuée très raisonnable.
Tableau 0. 1: Les pores irréguliers étudiés avec les approximations ellipsoïdales correspondantes ; erreur relative entre les tenseurs de contribution de souplesse et de résistivité numériques des pores irréguliers et ellipsoïdaux par rapport à la solution ellipsoïdale analytique (Eshelby pour le problème élastique et fonction implicite pour le problème thermique).
Estimation des propriétés effectives élastiques et thermiques du calcaire de Lavoux
Les propriétés effectives élastiques et thermiques sont évaluées pour un matériau contenant plusieurs pores de forme irrégulière d’une part et pour le même matériau avec de multiples pores ellipsoïdaux d’autre part. Les tenseurs de contribution de souplesse et de résistivité sont utilisés dans le cadre du schéma d’homogénéisation pour déterminer ces propriétés effectives. La phase solide du calcaire de Lavoux (grains micritiques à l’intérieur des oolites et du ciment entre les oolites) est principalement constituée de calcite pure. Par conséquent, la matière élastique de référence utilisée pour étudier la phase solide est la calcite pure.
En outre, la présence de pores dans les oolithes et dans la matrice du ciment nous permet de modéliser le calcaire de Lavoux comme suit (Giraud et al., 2015): (a) Oolite poreuse : calcite (micrite) + micro-pores (b) Matrice poreuse : calcite (sparite) + macro-pores. Une homogénéisation à deux étapes est donc appliquée (Figure 0.9). La première étape d’homogénéisation concerne les pores intra-oolithiques de forme sphérique dans les oolites en utilisant un schéma auto-cohérant (Bruggeman, 1935 ; Hill, 1965). Elle permet la transition de l’échelle microscopique à l’échelle mésoscopique.
La deuxième étape permet la transition de l’échelle mésoscopique à l’échelle macroscopique par le schéma d’homogénéisation de Maxwell. Le schéma d’homogénéisation de Maxwell (Maxwell, 1873) a été introduit pour la première fois dans le contexte de la conductivité électrique effective d’un matériau contenant plusieurs inhomogénéités sphériques. Maxwell a proposé une solution pour ce problème en comparant les résultats du champ lointain de la perturbation du champ électrique appliqué de l’extérieur calculé de deux façons différentes:
– Le champ lointain résultant est la somme de tous les champs lointains générés par toutes les inhomogénéités individuelles dans une région homogénéisée Ω.
– Le champ résultant à des points éloignés est égal au champ lointain généré par la grande région homogénéisée Ω avec des propriétés effectives inconnues.
A l’échelle mésoscopique, nous considérons que le milieu hétérogène est formé par trois phases : les oolites poreuses (o) approximées par des sphères, des macro-pores interoolithiques (b) approximés par des ellipsoïdes et du ciment inter-oolithique (ou calcite syntaxiale) (c) constitué de grains de calcite pure.
La Figure 0.10 montre les différents paramètres élastiques calculés en fonction de la porosité. Dans la Figure 0.11, les valeurs des modules de compressibilité élastique et de cisaillement pour un pore irrégulier sont comparées à la solution de l’approximation ellipsoïdale correspondante. Les propriétés élastiques effectives pour tous les autres pores et ellipsoïdes ont également été comparées. Dans tous les cas, les écarts des paramètres élastiques sont faibles et ne dépassent pas 5%.
De la même manière, la conductivité thermique du matériau contenant des pores irréguliers en fonction de la porosité est illustrée dans la Figure 0.12 (Gauche) alors que la Figure 0.12 (Droite) illustre la comparaison de la conductivité thermique dans les deux cas : pores irréguliers et ellipsoïdes. Comme dans le cas élastique, les résultats montrent un écart de 4% maximum.
En conclusion, l’approximation ACP des pores réels irréguliers est pertinente et son utilisation dans le cadre du schéma d’homogénéisation Maxwell est raisonnable.
Figure 0. 12: Gauche : Illustration de la conductivité thermique de 10 pores de forme irrégulière en fonction de la porosité en utilisant le schéma de Maxwell : chaque courbe correspond à un modèle contenant un des pores irréguliers orienté aléatoirement.
Droite : La conductivité thermique pour un pore sélectionné: vérification de l’approximation du pore de forme irrégulière par un ellipsoïde.
Conclusion et perspectives
L’analyse de la microstructure des roches oolithiques hétérogènes (calcaire de Lavoux et minerai de fer) par nanotomographie 3D à rayons X a montré que ces matériaux sont composés de la calcite subdivisée en 3 familles de tailles différentes : les oolithes, les pores inter-oolithiques 3D de forme irrégulière et le ciment interoolithique.
Dans le cadre du schéma d’homogénéisation de Maxwell, nous avons considéré un modèle simplifié pour ces roches où les oolithes sont approximées par des sphères et les pores par des ellipsoïdes. La méthode d’analyse en composantes principales a été utilisée pour effectuer ces approximations. Afin de vérifier l’approximation des oolithes, leur sphéricité a été calculée et les valeurs obtenues étaient proche de 1, ce qui permet de valider l’approximation des oolithes par des sphères.
Des essais de nanoindentation qui ont pour but d’identifier les propriétés micromécaniques du matériau, ont montré que le module d’élasticité des différents composants du calcaire de Lavoux varie entre 7 et 71 GPa. Des tests sur les oolithes, un microcalcite et un macrocalcite réalisé pour la première fois ont montré que les microcalcites sont les composants les plus durs du calcaire de Lavoux alors que les microcalcites sont les composants les moins durs.
Pour vérifier l’approximation dans le cas des pores irréguliers, les tenseurs de contribution d’une hétérogénéité isolée, contribution à la souplesse d’une part (problème élastique) et à la résistivité thermique d’autre part (problème de diffusion linéaire stationnaire), sont calculés numériquement par éléments finis. Ensuite, les tenseurs de contribution pour les pores ellipsoïdaux sont calculés par une solution analytique basée sur la solution d’Eshelby. L’erreur relative entre les tenseurs calculés produit un écart de l’ordre de 4,5% dans le problème élastique et 12% dans le problème thermique, ce qui rend raisonnable l’approximation des pores irréguliers par les ellipsoïdes en utilisant la procédure présentée.
Les propriétés effectives élastiques (module de compressibilité élastique et coefficient de cisaillement) et thermiques (conductivité thermique) ont été évaluées en fonction de la porosité en utilisant les tenseurs de contribution calculés pour les deux cas : pores irréguliers et ellipsoïdes. Les résultats obtenus sont à un bon accord avec un écart maximal de 5%.
Parmi les perspectives, on cite le développement des modèles micromécaniques en introduisant des informations microstructurales supplémentaires obtenues par des essais micromécaniques (nanoindentation par exemple pour le minerai de fer). Ensuite, une autre amélioration est l’augmentation du nombre de pores sélectionnés et la prise en compte des pores avec des niveaux d’irrégularité plus élevés.
Il serait pratique d’étendre la méthode numérique présentée à d’autres cas limitants, par exemple le cas humide, et de comparer les résultats obtenus avec les résultats expérimentaux.
Enfin, l’utilisation et la comparaison d’autres schémas d’homogénéisation et l’étude de leurs effets sur les propriétés effectives seraient intéressantes.
In general, the short and long-term behavior of rocks is modeled either by macro-mechanical (i.e., phenomenological) approaches or by micromechanical approaches. Micromechanical approaches have a particular and practical advantage since a relatively small number of assumptions are needed. In this case, the complexity of the simulated macroscopic behavior does not derive from the complexity of the introduced formalism, but rather from a few microstructural assumptions and statistical considerations on the constitutive elements (grains, crystals, pores, cracks).
The macroscopic thermomechanical behavior of the materials is largely affected by the microstructure. The micro-macroscopic relationship is described via micromechanical models developed within the framework of the homogenization theory of heterogeneous media (Maxwell homogenization method for example). The methods of homogenization (scale change) are used to define effective properties, elastic or conductive, on the « macroscopic » scale where the heterogeneous material can be considered as an equivalent homogeneous material. The aim of this work is then to study the influence of the microstructure of heterogeneous porous rocks on the behavior at the macroscopic scale.
The micro-macroscopic models used are enriched by microstructural data obtained from microscopic observations. Hence, the originality of this work is due to the unique combination of microstructural observations (SEM, X-ray 3D nano-tomography), multi-scale mechanical experiments (nano-indentation tests) and micro / macroscopic modeling. In addition, this work is innovative because it involves the study of natural materials (rocks) with realistic (heterogeneous) microstructures containing inhomogeneities (pores, cracks, inclusions) of different shapes, orientations and properties. Particular attention will be paid to oolitic porous rocks such as Lavoux limestone and iron ore, composed of an assembly of porous grains more or less spherical (oolites), pores and inter-granular crystals. These rocks were widely studied in GeoRessources laboratory as part of the feasibility study for the geological storage of carbon dioxide CO2 and the study of collapses of underground iron mines in Lorraine (France). Therefore, a detailed description of the mineralogical, petro-physical and hydromechanical properties of these rocks exists and it can be used as a reference in this work.
In Chapter I, we characterize the microstructure of the Lavoux limestone and the iron ore using three-dimensional imaging techniques such as scanning electron microscopy (SEM) and 3D computed nanotomography. X-Ray computed nanotomography allows distinguishing different components of considered rocks: porous network (size, spatial distribution and volume fraction), oolites and inter-oolite crystals. In addition, nano-indentation tests were performed to determine mechanical properties such as elastic parameters, which are necessary in homogenization models.
In Chapter II, we present statistical data describing several geometrical parameters (volume, radius, surface, sphericity, orientation…) of the components of considered rocks. We used a simplified model within the framework of Maxwell homogenization scheme where the porous oolites are approximated by spheres, and the pores of irregular shapes are approximated by ellipsoids. This approximation is performed using the Principal Component Analysis method (PCA), which provides the geometric properties such as the length of the semi-axes and the orientation of the resulting ellipsoids.
In Chapter III, we verify the approximation of irregularly shaped pores by ellipsoids by evaluating property contribution tensors of these pores. Thus, compliance contribution tensors for 3D irregular pores and their ellipsoidal approximations are calculated using the finite element method (FEM). These tensors were compared and a relative error is estimated to evaluate the accuracy of the approximation. The FEM numerical method is verified by comparing the numerical solution of compliance contribution tensors of the ellipsoids to the known analytical solution of these same shapes based on Eshelby’s theory.
In Chapter IV, the numerical method used in the elastic problem is extended to thermal conductivity problem, where the approximation of irregularly shaped pores is also verified by evaluating thermal resistivity contribution tensors. Calculated compliance and resistivity contribution tensors were used to compute effective elastic and thermal properties of a material containing irregularly shaped pores by a two-step Maxwell homogenization scheme. Finally, computed properties of a material containing irregularly shaped pores are compared to those of the same material containing ellipsoidal approximations to evaluate once again the accuracy of the approximation of irregularly shaped pores by tri-axial ellipsoids.
Table of contents :
Résumé de la thèse
0.1 Contexte général et problématique :
0.2 Objectifs de la thèse
03. Observations microscopiques et propriétés micromécaniques du calcaire de Lavoux et du minerai de fer
04. Approximation des formes irrégulières par des ellipsoïdes
04.1 Vérification de l’approximation des oolithes par des sphères
04.2 Vérification de l’approximation des pores irréguliers par des ellipsoïdes
0.5 Estimation des propriétés effectives élastiques et thermiques du calcaire de Lavoux.XXVII
0.6 Conclusion et perspectives
General Introduction
Microscopic observations and micromechanical properties of oolitic porous rocks
I.1 Introduction and description of the material
I.1.1 Description of the Lavoux limestone
I.1.2 Description of Iron ore
I.2 Nanoindentation tests:
I.2.1 Definition and background:
I.2.2 Function and equipment:
I.2.3 Mechanical properties measured by nanoindentation
I.2.4 Application of nanoindentation test on oolitic sample of Lavoux limestone
I.3 Computed X-Ray nanotomography:
I.3.1 Introduction and definition
I.3.2 Data acquisition and processing
I.3.3 Presentation of VGStudio MAX
I.3.4 Microstructural components of the Lavoux limestone and the iron ore
I.3.5 Porosity and representative elementary volume (REV)
Microstructural characterization of heterogeneous porous rocks (Lavoux limestone and Iron ore)
II.1 Approximation of irregular shapes by tri-axial ellipsoids
II.1.1 Introduction and theory
II.1.2 Approximation of irregularly shaped constituents using principle component analysis (PCA)
II.1.3 Surface reconstruction algorithms
II.2 Approximation of oolites by spheres: shape study and statistical analysis
II.2.1 Calculation of sphericity of oolites using selection tools
II.2.2 Calculation of sphericity of oolites using grinding process
II.3 Approximation of pores by tri-axial ellipsoids
II.3.1 Statistical data of porous network
II.3.2 Extraction of 3D irregularly shaped pores from nanotomography data
II.3.2 Application of the PCA on the extracted pores
Compliance contribution tensor of 3D irregularly shaped pores
III.1 The first and second Eshelby problems
III.1.1 The first problem of Eshelby for ellipsoidal inclusion
III.1.2 The second problem of Eshelby for ellipsoidal inhomogeneities
III.2 Validation of the approximation of irregular pores by ellipsoids using compliance contribution tensors
III.2.1 Numerical method for compliance contribution tensor of irregular pore and its ellipsoidal approximation
III.2.2 Numerical integration on the inhomogeneity surface (3D modelling)
III.2.3 Analytical evaluation of compliance contribution tensor of approximated ellipsoids
III.2.4 Fobenius norm: relative error between numerical and analytical methods
III.3 Effect of geometrical parameters on compliance contribution tensors
III.3.1 Effect of mesh size
III.3.2 Effect of pore volume and surface area on compliance contribution tensor
Determination of effective properties with Maxwell homogenization scheme
IV.1 Estimation of the effective elastic and conductive properties of the Lavoux limestone
IV.1.1 Homogenized model for effective properties
IV.1.2 Application of Maxwell homogenization scheme to determine effective elastic properties
IV.2 Application of Maxwell homogenization scheme to determine conductive properties.. 104
IV.2.1 Resisitivity contribution tensors of 3D irregularly shaped pores
IV.2.2 Maxwell homogenization scheme reformulated in terms of resistivity contribution tensors
Conclusion and Perspectives